Logistic Regression for Machine Learning
 Naveen
Naveen- 0
Logistic Regression is one of the most used Machine learning algorithms among industries and academia. It is a supervised learning algorithm used for classification where the target variable should be categorical.
Why not Linear Regression for classification
There are mainly two reasons for not fitting a linear regression on classification tasks:
- When we fit a linear regression model, it will never be confined in the range 0 and 1. But the target variables are probabilities, so we cannot allow our model to go in the range of > 1 and < 0.
- Suppose the data is highly biased towards one class, i.e., the number of samples of class 1 >> the number of samples of class 2. In such a case, our Linear line will be more inclined towards class 1. Hence accuracy will suffer a lot.
Assumptions
- Assumes a linear relationship between the logit of the independent variables and dependent variable.
- Normal distribution is not assumed for the dependent variable as well as for errors.
- Absence of multi-collinearity.
- Larger samples are needed than for linear regression.
- The dependent variable must be dichotomy(2categories).
Derivation
For linear regression, the equation is given by
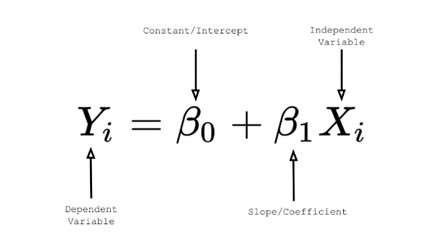
To avoid the failure of Linear Regression, we fit the probability function p(x) that can only have values between 0 and 1.
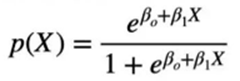
After rearranging, we will get
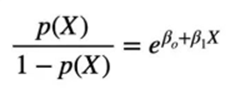
Taking log on both side
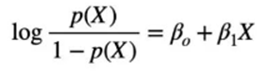
This look similar to Linar Regression problem where we can fit the logit function. The y-values from the original linear regression model are transformed using the logit function.
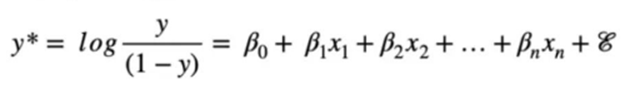
Decision boundary
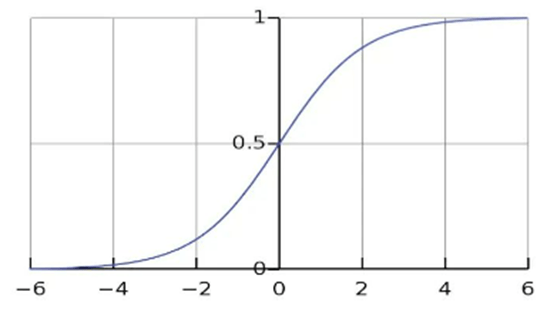
We can say that the linear regression fits the linear function, but logistic regression fits the sigmoid function.
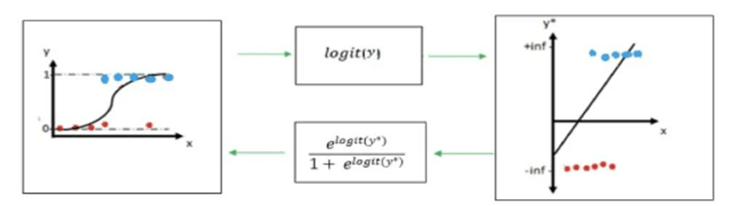
The decision boundary selected based on the threshold value (default 0.5). for example, if p(X) >= 0.5, it will be mapped to class 1 otherwise class 0. The threshold value can be changed depend on the problem statement and requirement.
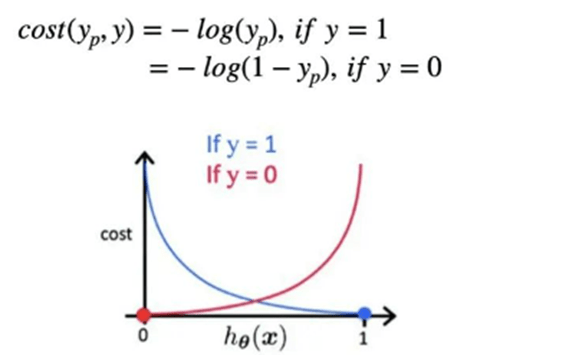
Loss function
We can not use RMSE or Sum-squared error as a loss function in Logistic regression as function will be non-convex, and primarily it will land in the local optima.
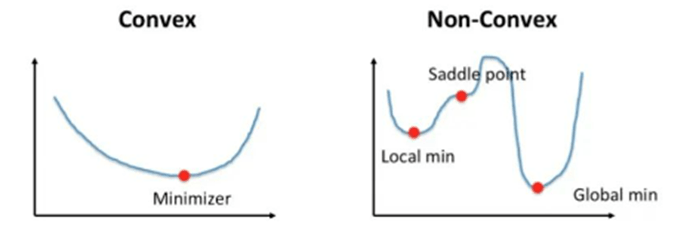
To avoid the problem of RMSE or MSE, we adopt maximum Likelihood Estimation i.e., MLE for this type of regression problem. After MLE the cost function is given by: