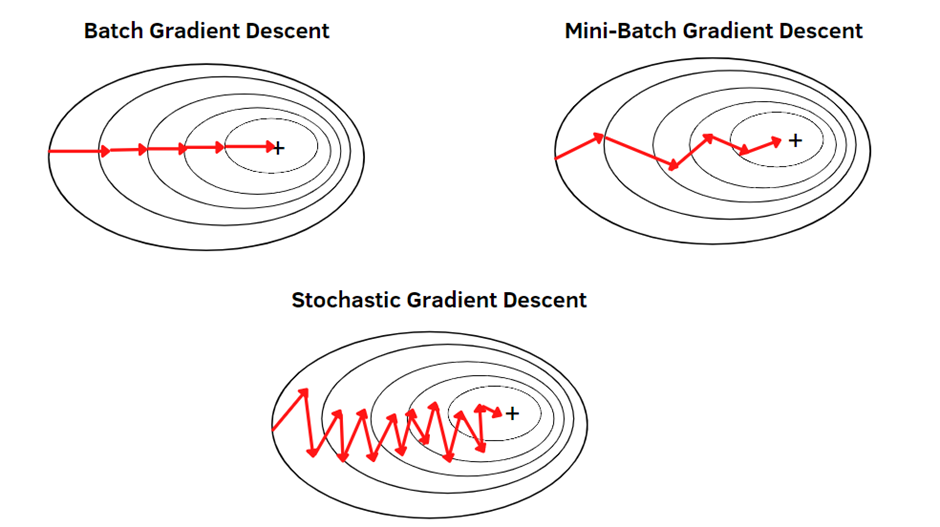
What is GD, Batch GD, SGD, Mini-Batch GD?
 Naveen
Naveen- 0
What is Gradient Descent, Batch Gradient Descent, Stochastic Gradient Descent, Mini-Batch Gradient Descent?
Gradient Descent
This algorithm is a general algorithm that is used for optimization and for providing the optimal solution for various problems. It takes parameters in an iterative way and makes the cost function as simple as possible.
1) Define a cost function, c(x).
2) Iterate to find the optimal solution using x1 , x2, x3, …xn.
3) Compare the current value of the cost function to the optimal value and make a decision as to whether to stop iterating or not.
4) If not stopping then go back to step 3 and iterate.
5) return the optimal solution.
Using a gradient descent (“like falling down a hill”) algorithm, this will measure the errors. But even though you’ll calculate the minimum, it won’t need to go to that extreme–you’ll hit the first plateau.

Also, you should keep in the mind that the size of the steps is very important for this algorithm, because if it’s very small – “meaning the rate of learning” is slow – it will take a long time to cover everything that it needs to.
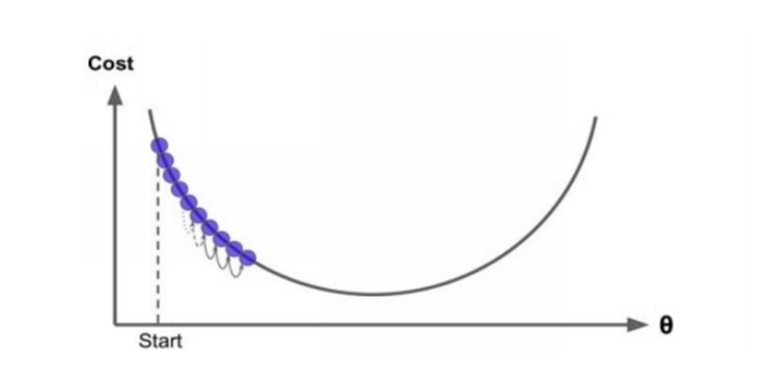
But when the rate of learning is high, It will take short time to cover what’s needed, and it will provide an optimal solution.
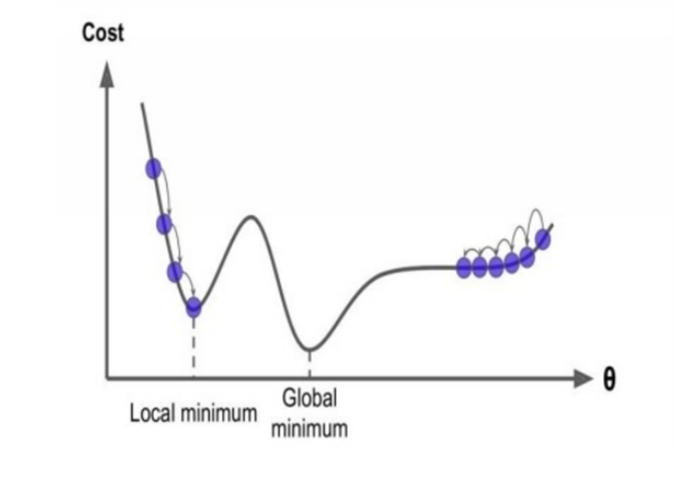
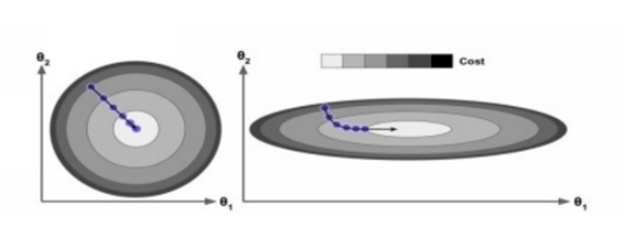
At the end, you won’t always find that all cost functions are easy, as you can see, but you’ll also find irregular functions that make getting an optimal solution very difficult. This problem occurs when the local minimum and global minimum looks like they do in the following figure.
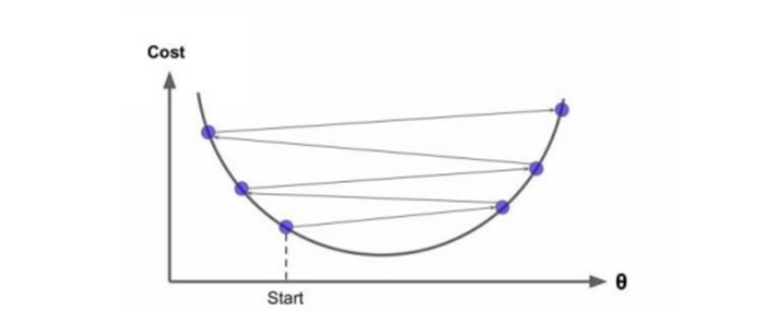
If you assign any to any two points on your curve, you’ll find that the segment of the line won’t join them on the same curve. This cost function will look like a bowl, which will occur if the features have many scales, as in the following image.
Batch Gradient Descent
To calculate the gradient of your cost function, you should first make sure that you have theta parameter inputted. If the value of the parameter has changed, you’ll need to know how it changes your cost function. What we can refer to as “change” could also be a derivative. It is sometimes calculated using the following equation:
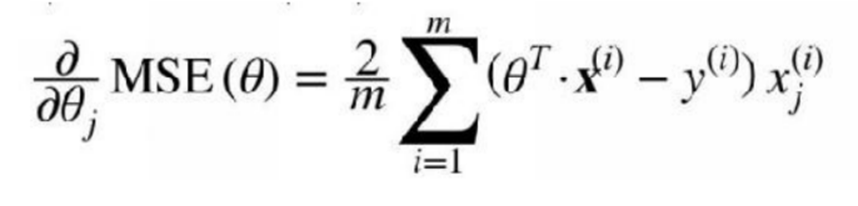
But we`ll also use the following equation to calculate the partial derivatives and the gradient vector together.
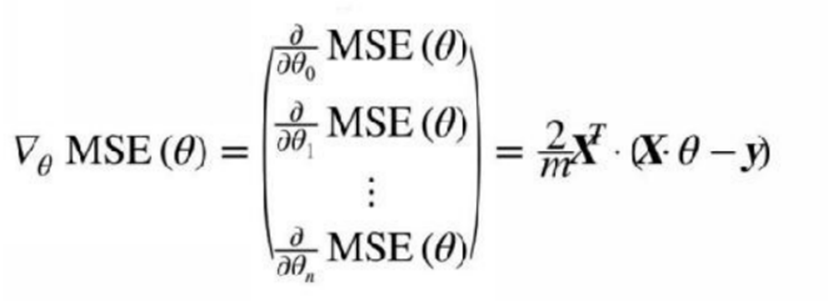
Let’s implement the algorithm.
Lr = 1 # Lr for learning rate
Num_it = 1000 # number of iterations
L = 100
myTheta = np.random.randn (2,1)
for it in range(Num_it):
gr = 2/L * Value1.T.dot(Value1.dot(myTheta) – V2_y)
myTheta = myTheta – Lr * gr
>>> myTheta
Array([[num], [num]])
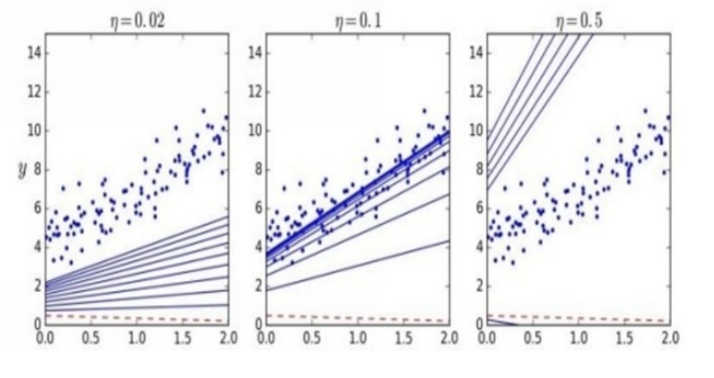
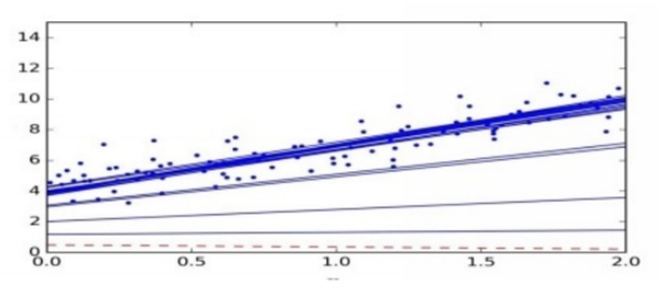
If you try to change the learning rate value, you’ll get different shapes, as in the following figure.
Stochastic Gradient Descent
It can be difficult to know where to spend time training your model, especially if you’re not sure whether you have enough data for optimal performance. The only way to make sure the full training set is used for each step is by using batch gradient descent.
But when using the stochastic gradient descent, the algorithm will randomly choose an instance from your training set at each step and then calculate the values. In this way, the algorithm will tend to be faster than the batch gradient descent that needs to use all of the data at once, but it will not be as regular as batch methods would.
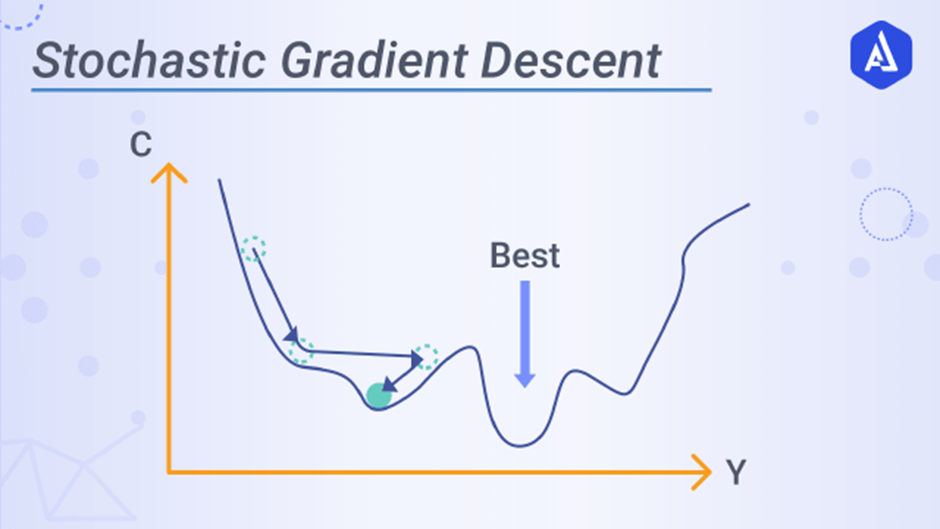
Let’s implement the algorithm.
Nums = 50
L1, L2 = 5, 50
Def lr_sc(s):
return L1 / (s + L2)
myTheta = np.random.randn(2,1)
for Num in range (Nums):
for l in range (f)
myIndex = np.random.randint(f)
V1_Xi = Value1[myIndex:myIndex+1]
V2_yi = V2_y[myIndex:myIndex+1]
gr = 2 * V1_xi.T.dot(V1_xi.dot(myTheta) – V2_yi)
Lr = lr_sc(Num * f + i)
myTheta = myTheta – Lr * gr
>>> myTheta
Array ([[num], [num]])
Mini-Batch Gradient Descent
Being able to understand a batch gradient machine learning algorithm is much simpler than it sounds. You’ll find that the algorithms provide quality training data for your model so that you can start using it immediately, saving time and effort. Mini-batch algorithms are good for small organizations that prefer not to conduct ongoing analyses, but it does not compare favorably to the other two AI algorithms.