Nomidl

Support Vector Machine algorithm for Machine Learning

• Naveen
• October 3, 2022December 12, 2024
• 0

• Support vector Machine or SVM is a Supervised Learning algorithm, which is used for Classification and Regression problems. However, primarily, it is used for classification problems in Machine Learning.
  
• The goal of the SVM algorithm is to create the decision boundary that can segregate n-dimensional space into classes so that we can easily classify new data points in the correct category. The best decision boundary is called a hyperplane.

Terminologies

• Hyperplane: There can be multiple decision boundaries to segregate the classes in n-dimensional space, but we need to find out the best decision boundary that helps to classify the data points. This best boundary is known as the hyperplane of SVM that has a maximum margin, which means the maximum distance between the data points.
  
• Support Vectors: The data points or vectors that are the closest to the hyperplane and which affect the position of the hyperplane are termed as Support Vector. Since these vectors support the hyperplane, hence called a Support Vector.

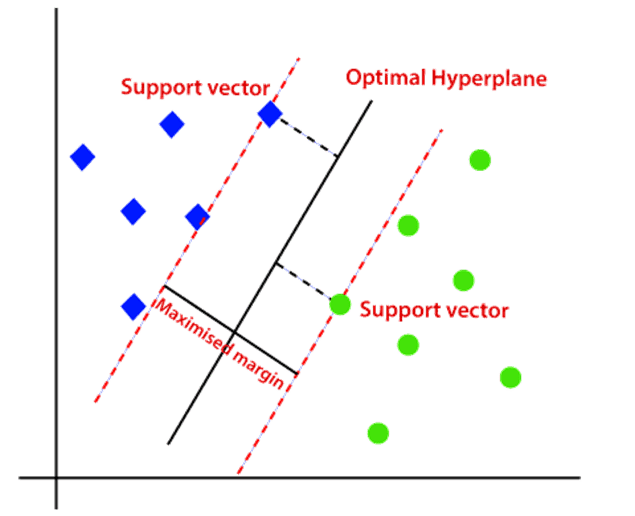
Linear SVM: Algorithm Working

• Suppose we have a dataset with two features x1 and x2 and there are two classes blue and green.

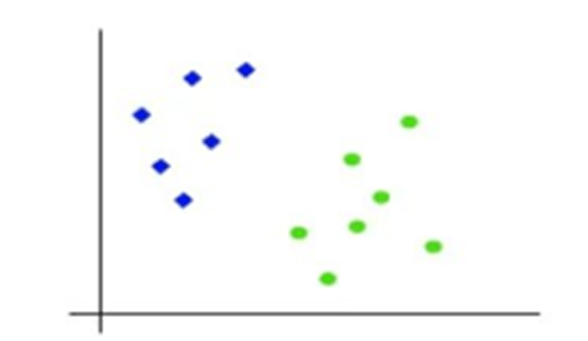
• So, as it is 2-d space so by just using a straight line, we can easily separate these two classes. But there can be multiple lines that can separate these classes.

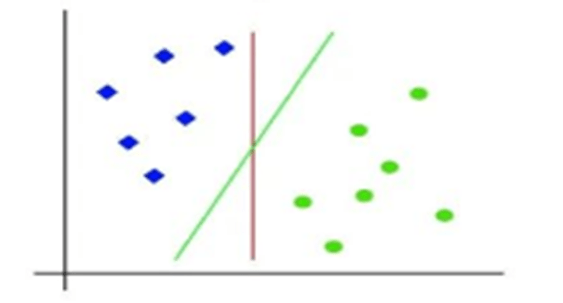
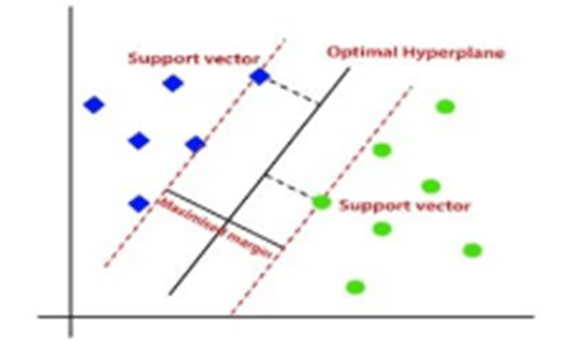
• The SVM algorithm helps to find the best decision boundary called optimal Hyperplane by maximizing the marginal distance between support vectors and hyperplane.

Non-Linear SVM: Working

• For non-linear data, we cannot draw a single straight line.

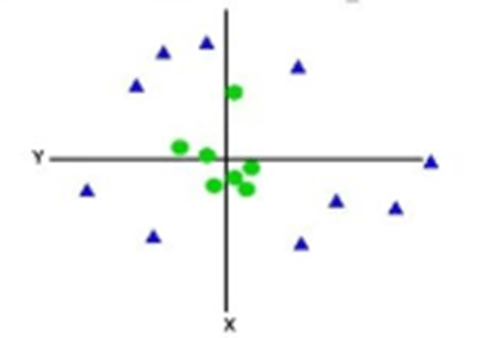
• So to separate these data points, we need to add one more dimension. It can be calculated as:

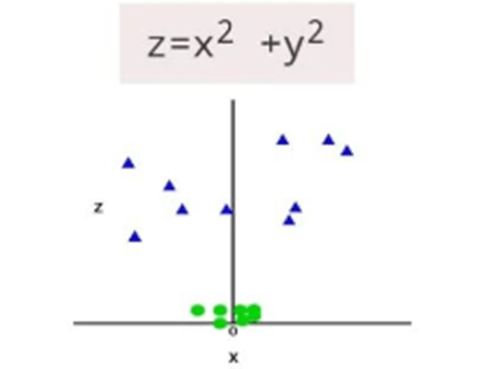
• So now, SVM will divide the dataset into classes in the following way. Since we are in 3-d space, hence it is looking like a plane parallel to this x-axis.

Advantages & Disadvantages

Advantages:

• It works really well with a clear margin of separation.
• It is effective in high dimensional space
• It is effective in cases where the number of dimensions is greater than the number of samples.
• Different kernel functions can be specified for the decision function.

Disadvantages:

• It doesn’t perform well when we have large data set because the required training time is higher.
• It also doesn’t perform very well, when the data set has more noise i.e., target classes are overlapping.
• SVM doesn’t directly provides probability estimates, these are calculated using an expensive five-fold cross-validation.

Popular Posts