10 Advanced NumPy Functions You Need to Know
 Naveen
Naveen- 0

Numpy is a powerful Python library for scientific computing and data analysis. It provides a wide range of functions and tools for manipulating multidimensional arrays and matrices.
In this blog post, we’ll talk discuss 10 advanced Numpy features you should know to get the most out of this library.
1 – np.linspace()
The np.linspace() function creates a specified number of evenly spaced values in a specified range. To create, you need the starting and ending values of the interval and the number of points. Here is an example. Here’s an example:

2 – np.logspace()
The np.logspace() function generates a fixed number of logarithmically spaced values in a given range. To create, you need the starting and ending exponent of the range and the number of points. let’s see an example:

3 – np.broadcast()
The np.broadcast() function broadcasts arrays of different shapes and sizes in a common shape. This can be useful when performing arithmetic operations on array of different shapes. let’s see an example:

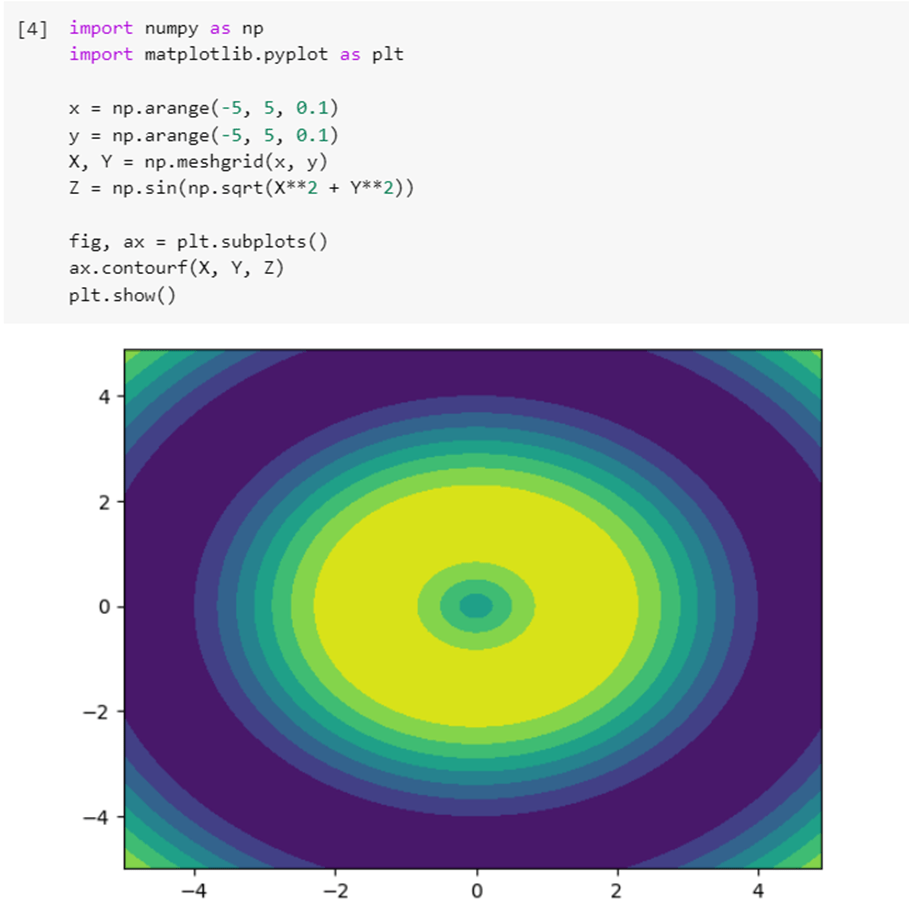
4 – np.meshgrid()
The np.meshgrid() function creates a grid of points from two or more coordinate vectors. This can be useful when plotting surfaces or contours. Let’s an example:
5 – np.unique()
The np.unique() function returns the unique elements of an array. It also has an optional argument to return the indices of the unique elements. Let’s an example:

6 – np.pad()
The np.pad() function pads an array with a specified number of values at the beginning and end of each axis. This can be useful when we need to resize an image or padding sequences.

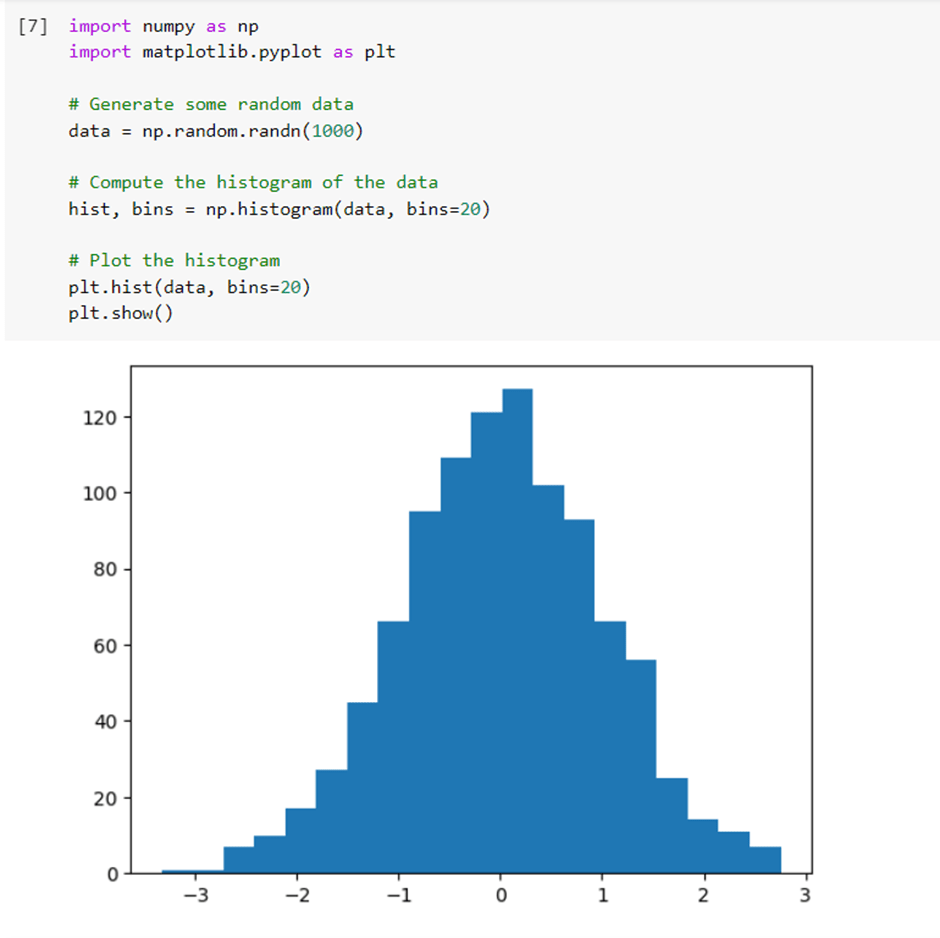
7 – np.histogram()
The np.histogram() function computes the histogram of an array. A histogram represents the distribution of a dataset by dividing it into a set of intervals (called “bins”), counting the number of values that fall into each bin, and plotting the result. Here’s an example:
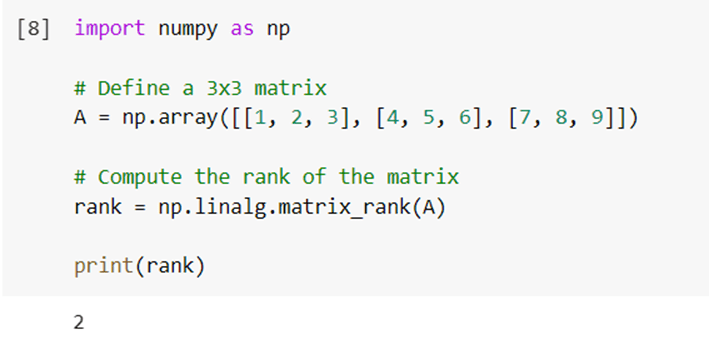
8 – np.linalg.matrix_rank()
The np.linalg.matrix_rank() function computes the rank of a matrix. The rank of a matrix is the number of linearly independent rows or columns in the matrix. Here’s an example:
9 – np.linalg.solve()
The np.linalg.solve() function solves a system of linear equations of the form Ax = b, where A is a matrix and b is a vector. Let’s an example:

10 – np.linalg.eig()
The function np.linalg.eig() calculates the eigenvalues and eigenvectors of a square matrix. Eigenvectors are vectors that are scaled only by a scalar factor when multiplied by a matrix, and eigenvalues are scaling factors by which eigenvectors are scaled. Let’s an example:

Conclusion
In this article we have seen 10 Advanced NumPy function and implemented them in Python.
