Nomidl

Decision Tree for Machine Learning

• Naveen
• September 18, 2022July 5, 2023
• 2

Tree based algorithms are a popular family of related non-parametric and supervised methods for both classification and regression.

The decision tree looks like a upside-down tree with a decision rule at the root, from which subsequent decision rules spread out below.

Sometimes decision trees are also referred to as CART, which is short for classification and Regression Trees.

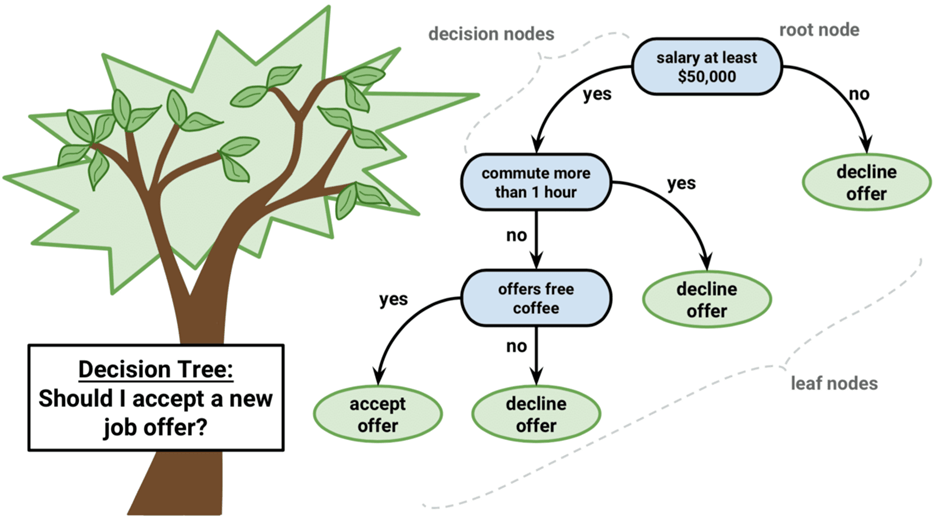
Types of Decision Trees:

1. Categorical Variable Decision Trees.
2. Continuous Variable Decision Trees.

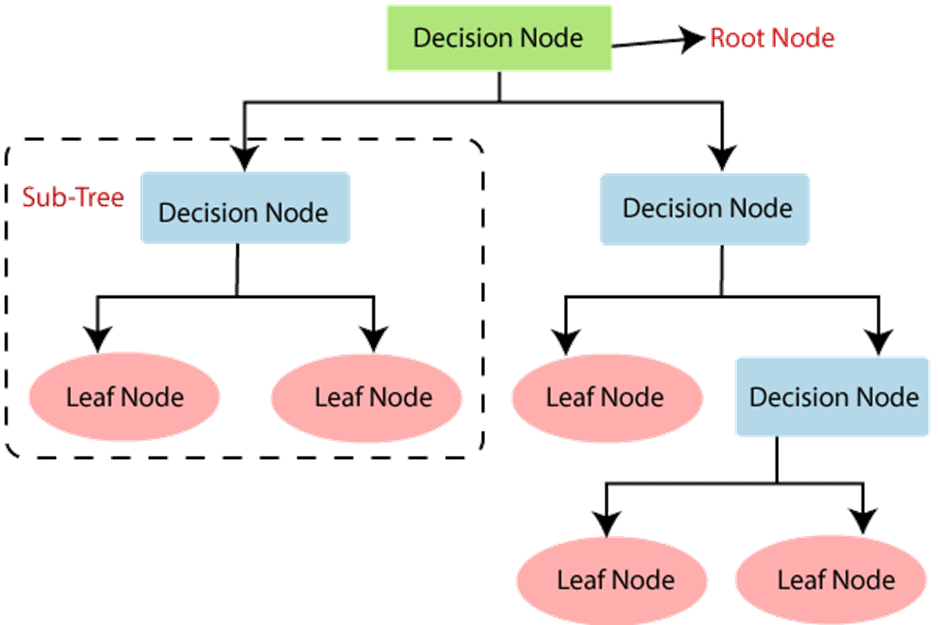
Terminologies

1. Every tree has a root node, where the inputs are passed through.
2. this root node is further divided into sets of decision nodes where results and observations are conditionally based.
3. the process of dividing a single node into multiple nodes is called splitting.
4. if a node doesn’t split into further nodes, then it’s called a leaf node, or terminal node.
5. A subsection of decision tree is called a branch of sub-tree.

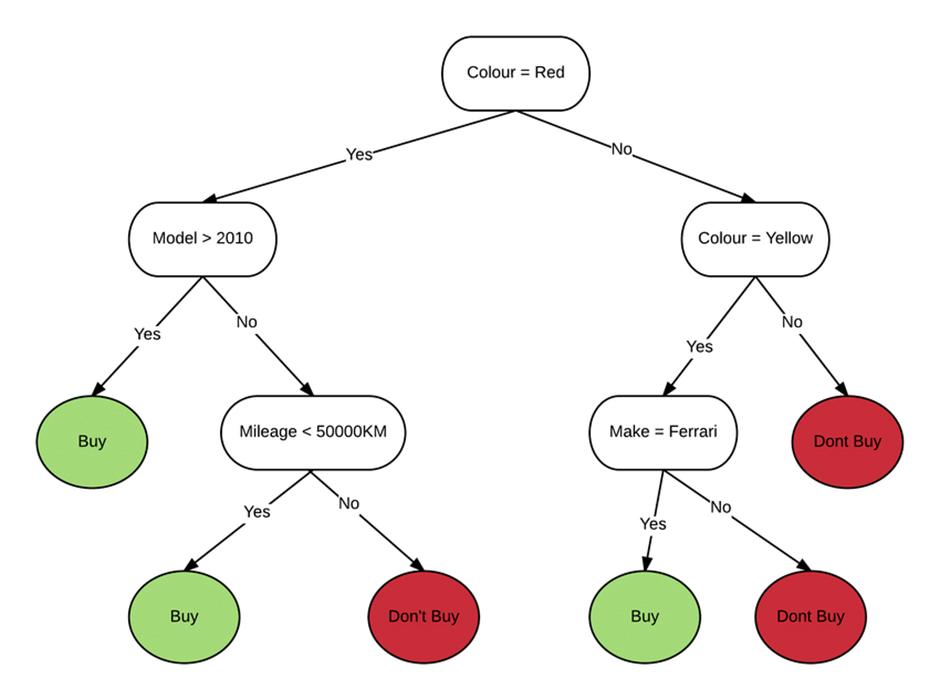
Algorithm Working

Step-1: Begin the tree with root node, says S, which contains the complete dataset.

Step-2: Find the best attribute in the dataset using a selection criteria.

Step-3: Divide the S into subsets that contains possible values for the best attributes.

Step-4: Generate the decision tree node, which contains the best attribute.

Step-5: Recursively make new decision trees using the subsets of the dataset created in step-3.

Continue this process until a stage is reached where you cannot further classify the nodes and called the final node as a leaf node.

Attribute selection criteria

While implementing a decision tree, the main concern is how to select the best attributes for the root node and for sub-nodes and to solve such problems we use selection criteria by which we can easily select the best attribute for the nodes. There are two popular techniques used for attribute selection:

• Gini index: the measure of the degree of probability of a particular variable being wrongly classified when it is randomly chosen is called the Gini index or Gini impurity.
• Information Gain: Entropy is the main concept of this algorithm, which helps determine a feature or attribute that gives maximum information about a class is called information gain.

Advantages and Disadvantages

Advantages

• Decision trees are easy to visualize.
• Non-linear pattern in the data can be capture easily.
• It can be used for predicting missing values, suitable for feature engineering techniques.

Disadvantages

• Over-fitting of the data is possible
• The small variation in the input data can result in a different decision tree. This can be reduced by using feature engineering techniques.
• We have to balance the data-set before training the model.

Popular Posts