What is Tanh activation function?
 Naveen
Naveen- 0
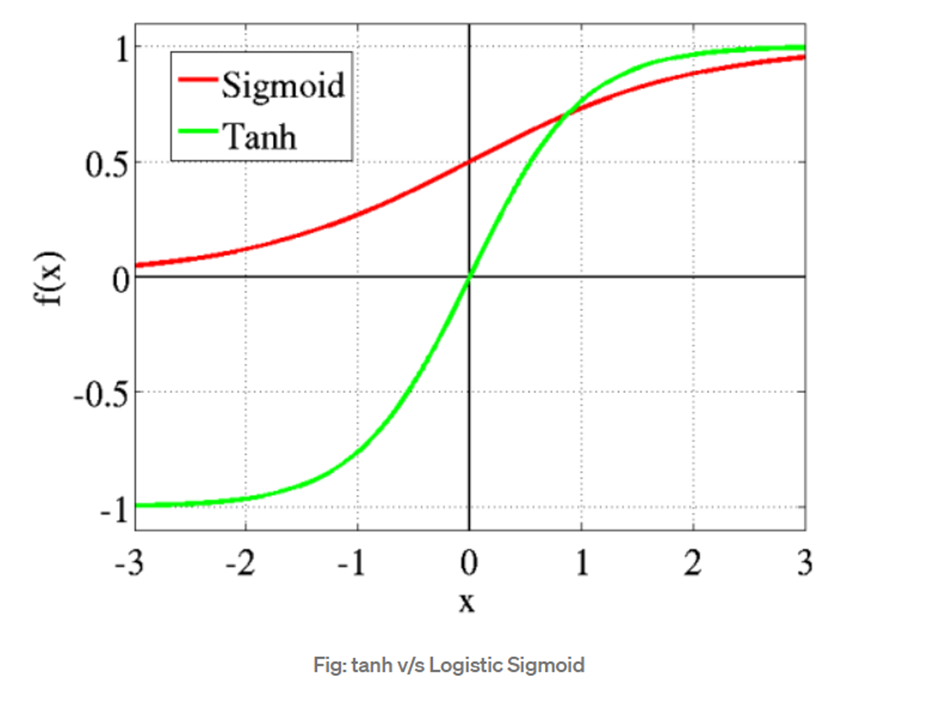
The Tanh Activation function is a scaled and shifted version of the hyperbolic tangent function, a mathematical function frequently encountered in trigonometry and calculus. The Tanh function squashes input values within the range of -1 to 1, making it a useful choice for activation functions in neural networks.
Defining the Tanh Function Mathematically
The mathematical formulation of the Tanh Activation function is as follows:

The function’s output is bounded between -1 and 1, with the inflection point at x = 0. This means that the Tanh Activation function produces positive outputs for positive input values and negative outputs for negative input values, mapping the input range to the (-1, 1) interval.
The Role of the Tanh Activation Function in Neural Networks
Why is the Tanh Activation Function Popular in Neural Networks?
The Tanh Activation function is widely used in neural networks due to its centered, zero-mean output, which helps mitigate the vanishing gradient problem that occurs with the sigmoid activation function. Additionally, the zero-centered property facilitates faster convergence during the training process, as it avoids biasing the updates in one particular direction.
Advantages of Using the Tanh Activation Function
The Tanh Activation function comes with several advantages, making it a popular choice in various applications:
1. Zero-Centered Output
The Tanh function produces a symmetric output around zero, which helps prevent the vanishing gradient problem and facilitates more stable learning in neural networks.
2. Output Range
The function maps input values to a range between -1 and 1, making it suitable for tasks that require a balanced output.
3. Non-Linearity
Like other activation functions, the Tanh Activation function introduces non-linearity to neural networks, enabling them to learn complex patterns and relationships in data.
4. Universal Approximation
The Tanh Activation function contributes to the universal approximation theorem, demonstrating its ability to approximate any continuous function given sufficient hidden units in a neural network.
Limitations of the Tanh Activation Function
As with any activation function, the Tanh function also has some limitations that need to be considered:
1. Vanishing Gradient
While the Tanh function reduces the vanishing gradient problem compared to the sigmoid function, it may still suffer from this issue in very deep neural networks.
2. Exploding Gradient
In certain situations, the Tanh function can lead to an exploding gradient problem, causing instability during training.
3. Centered Output Bias
The zero-centered output of the Tanh function may introduce biases in the learning process for certain tasks and architectures.
Practical Applications of the Tanh Activation Function
The Tanh Activation function finds applications in various domains, including:
1. Natural Language Processing (NLP)
In NLP tasks such as sentiment analysis, language translation, and text generation, the Tanh Activation function can effectively handle output predictions within the (-1, 1) range.
2. Image Processing
In image-related tasks like image classification and object detection, the Tanh Activation function can be employed to normalize the output probabilities.
3. Recurrent Neural Networks (RNNs)
The Tanh Activation function is a popular choice in RNNs due to its suitability for processing sequential data, such as in speech recognition and time series analysis.
Implementing the Tanh Activation Function
Python Implementation of the Tanh Function
To implement the Tanh Activation function in Python, you can use the tanh function from popular libraries like NumPy or TensorFlow.
import numpy as np
def tanh_activation(x):
return np.tanh(x)
Conclusion
In conclusion, the Tanh Activation function is one of the important activation function of neural network. Its zero-centered output, output range, and non-linearity make it a popular choice for various machine learning tasks. Understanding its advantages and limitations you will be able to use it effectively and apply in your neural network architectures
