Nomidl

What is L1 and L2 regularization in Deep Learning?

• Naveen
• April 17, 2022December 12, 2024
• 0

In deep learning, L1 and L2 regularization are regularization techniques used to penalize the model’s weights during the training process. This penalty discourages the model from assigning excessive importance to certain features, thereby reducing the risk of overfitting.

L1 Regularization

L1 regularization, also known as Lasso regularization, adds a penalty proportional to the absolute value of the weights. Mathematically, it adds the sum of the absolute values of the weights to the loss function:

                    L1 regularization term = λ * Σ|wi|

where λ is the regularization parameter, and wi represents the individual weights.

The L1 regularization is effective in inducing sparsity in the model by driving some of the weights to zero. Consequently, it acts as a feature selection method, where less important features are removed from the model, leading to a simpler and more interpretable model.

L2 Regularization

L2 regularization, also known as Ridge regularization, adds a penalty proportional to the square of the weights. Mathematically, it adds the sum of the squared weights to the loss function:

                      L2 regularization term = λ * Σ(wi^2)

where λ is the regularization parameter, and wi represents the individual weights.

Unlike L1 regularization, L2 regularization does not induce sparsity. Instead, it shrinks the weights towards zero without setting them exactly to zero. This results in a model that considers all features but reduces their overall impact on the final prediction.

Importance of Regularization in Deep Learning

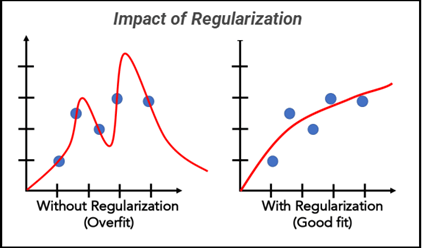
Deep learning models are highly susceptible to overfitting, especially when dealing with complex and large datasets. Overfitting occurs when a model performs well on the training data but fails to generalize to unseen data. Regularization helps combat overfitting by constraining the model’s flexibility during training.

By adding the regularization term to the loss function, the model learns to strike a balance between fitting the training data and keeping the weights small. As a result, the model becomes less sensitive to noise and minor fluctuations in the training data, leading to better generalization on unseen data.

Advantages of Using L1 and L2 Regularization

Both L1 and L2 regularization techniques offer unique advantages in deep learning models:

Advantages of L1 Regularization

1. Feature Selection: L1 regularization can drive some weights to exactly zero, effectively performing feature selection and making the model more interpretable.
2. Sparse Models: L1 regularization induces sparsity, resulting in models with fewer parameters and reduced memory and computational requirements.
3. Outlier Robustness: L1 regularization is more robust to outliers in the data due to its absolute value penalty, making it suitable for datasets with noise.

Advantages of L2 Regularization

1. Continuous Impact: L2 regularization does not lead to feature selection, and all features contribute to the prediction, albeit with reduced impact.
2. Stability: L2 regularization provides more stable training by preventing dramatic changes in the weights during optimization.
3. Better Generalization: L2 regularization helps improve generalization performance by reducing the risk of overfitting.

L1 vs. L2 Regularization: Key Differences

L1 and L2 regularization differ in several key aspects:

1. Penalty Type: L1 regularization penalizes the absolute value of weights, while L2 regularization penalizes the squared values of weights.
2. Sparsity: L1 regularization induces sparsity, while L2 regularization does not set weights exactly to zero.
3. Feature Importance: L1 regularization performs feature selection, prioritizing important features, while L2 regularization retains all features.
4. Computational Cost: L1 regularization is computationally more expensive due to the non-differentiability at zero weights.

Implementation L1 and L2 Regularization in Deep Learning Models

To apply L1 and L2 regularization to a deep learning model, we simply add the regularization term to the loss function. The regularization parameter λ controls the strength of the regularization, and its value needs to be chosen carefully through hyperparameter tuning.

Using libraries like TensorFlow or PyTorch, incorporating L1 and L2 regularization is straightforward. For example, in TensorFlow, we can add regularization to a dense layer as follows:

from tensorflow.keras.layers import Dense
from tensorflow.keras.regularizers import l1, l2

model.add(Dense(64, activation='relu', kernel_regularizer=l1(0.01)))

Conclusion

In conclusion, L1 and L2 regularization are powerful techniques in the realm of deep learning to tackle overfitting and improve model generalization. L1 regularization induces sparsity and feature selection, whereas L2 regularization shrinks weights to avoid overfitting without removing features. Both techniques have their unique benefits, and the choice between them depends on the specific requirements of the problem.

Popular Posts